- Stanford University
Abstract
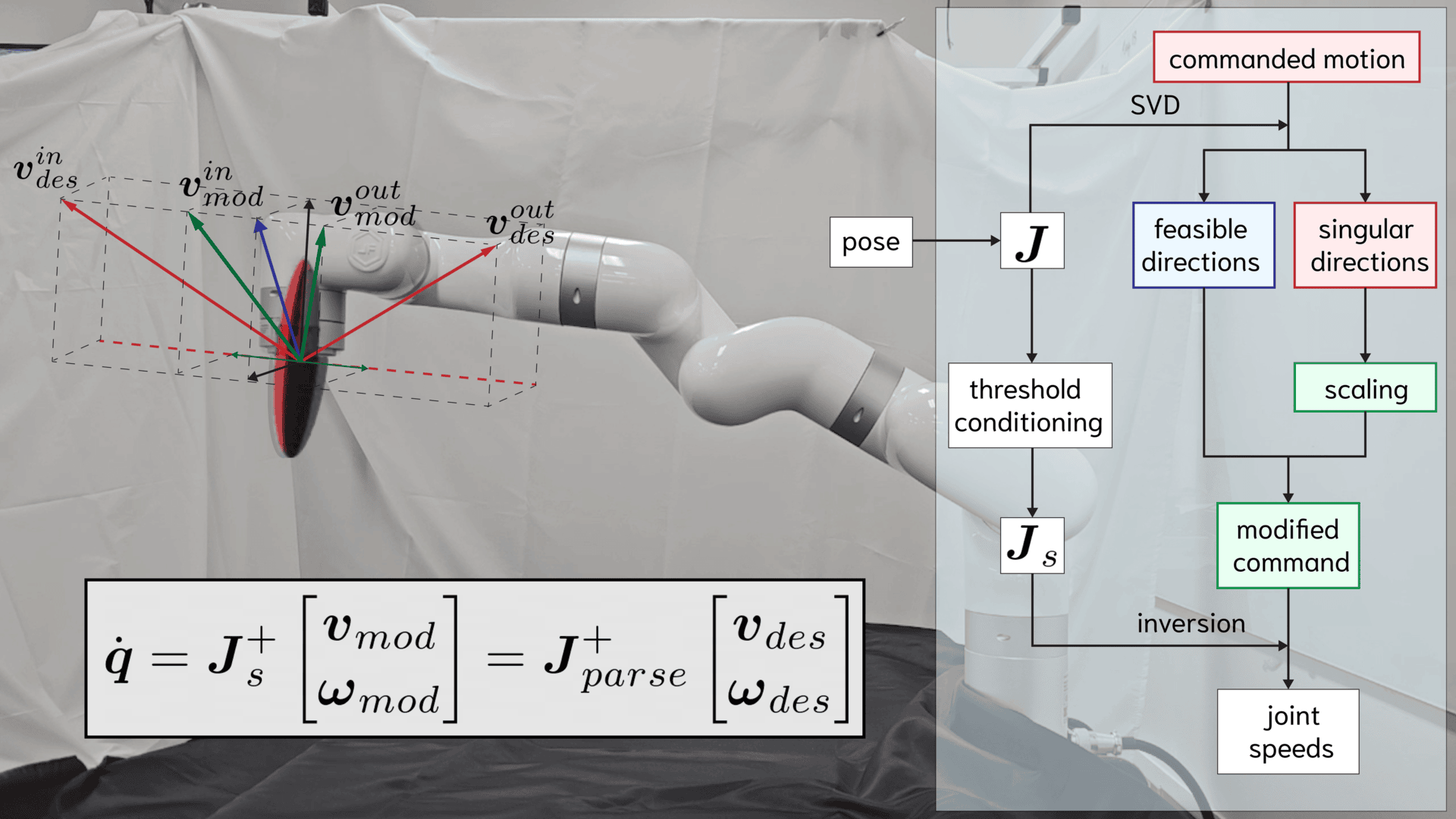
J-PARSE is a method for smooth first-order inverse kinematic control of a serial manipulator near kinematic
singularities. The commanded end-effector velocity is interpreted component-wise, according to the available
mobility in each dimension of the task space. First, a substitute "Safety" Jacobian matrix is created,
keeping the aspect ratio of the manipulability ellipsoid above a threshold value. The desired motion is then
projected onto non-singular and singular directions, and the latter projection scaled down by a factor
informed by the threshold value. A right-inverse of the non-singular Safety Jacobian is applied to the
modified command. In the absence of joint limits and collisions, this ensures smooth transition into and out
of low-rank poses, guaranteeing asymptotic stability for target poses within the workspace, and stability for
those outside. Velocity control with J-PARSE is benchmarked against the Least-Squares and Damped Least-Squares
inversions of the Jacobian, and shows high accuracy in reaching and leaving singular target poses. By
expanding the available workspace of manipulators, the method finds applications in servoing, teleoperation,
and learning.
Lay Explanation
What is the problem?
When robots are in awkward poses called singularities, they have trouble moving in certain directions. For example, when they are almost fully stretched out, it's hard to move in or out, and much easier to move sideways. When a human operator specifies a speed and direction for the robot hand, without accounting for this, the joints start spinning wildly in an effort to achieve the impossible.
What was the most common solution?
Most existing controllers avoid such configurations, either by slowing down and stopping before they occur, or by letting the joints speed up until a point and then suddenly going into emergency-stop mode. Neither approach is intuitive for users and neither allows the robot to make use of its full reachable space.
What do we propose instead?
We propose a modification that lets the robot continue moving as best it can, even if asked to enter or leave a singular pose. The idea behind the modification is: in the direction in which the hand can move easily, it should move as asked; in the other direction, the motion request should be diminished. The harder it is to move in that direction, the lower the speed that should be asked of it in that direction. By selectively slowing down, it becomes possible to keep the joints moving stably and still reach any reachable pose. But the robot should not be asked to stop -- neither in that direction nor any other -- just because it is close to singularity.
What makes this relevant now?
Traditionally, robots were used for repetitive tasks in industry. It was important to be fast and accurate in following preprogrammed motion requests. Handcrafting the location of the assembly line in order to avoid singularities was no problem. Today, when humans interact closely with robotic arms in everyday settings, it is much more important for robots to reach where they are asked to reach and to move in predictable ways. It is much more acceptable to slow down if necessary, rather than to simply "stop trying" in response to certain requests.
Is there a simple analogy?
A child (or for that matter, an adult) is good at one activity and finds another extremely daunting. The goal is for this child to achieve a task that relies on successful completion of both activities. As a teacher, the options are:
1. Insist on both parts being completed in a short period of time. The child's confidence is shattered and neither part gets done. In fact everything goes downhill after this. Even bystanders suffer.
2. Decide that nothing can be done about the task as a whole. Instruct the child not to attempt it. The task remains undone and the skill unlearned. The child never even finds out what was possible.
3. Explain that the task has two parts. The first part can and should be done, and will move fast and be done well. For the second part, ask first for only a start, a small piece of the job. Once the start is made, ask for a little more, something manageable. Explain that there is enough time to learn and do just that piece for now. Keep breaking the activity into parts and stepping through it piece by piece. In time, the entire task will be completed, and the child's capabilities expanded.
When robots are in awkward poses called singularities, they have trouble moving in certain directions. For example, when they are almost fully stretched out, it's hard to move in or out, and much easier to move sideways. When a human operator specifies a speed and direction for the robot hand, without accounting for this, the joints start spinning wildly in an effort to achieve the impossible.
What was the most common solution?
Most existing controllers avoid such configurations, either by slowing down and stopping before they occur, or by letting the joints speed up until a point and then suddenly going into emergency-stop mode. Neither approach is intuitive for users and neither allows the robot to make use of its full reachable space.
What do we propose instead?
We propose a modification that lets the robot continue moving as best it can, even if asked to enter or leave a singular pose. The idea behind the modification is: in the direction in which the hand can move easily, it should move as asked; in the other direction, the motion request should be diminished. The harder it is to move in that direction, the lower the speed that should be asked of it in that direction. By selectively slowing down, it becomes possible to keep the joints moving stably and still reach any reachable pose. But the robot should not be asked to stop -- neither in that direction nor any other -- just because it is close to singularity.
What makes this relevant now?
Traditionally, robots were used for repetitive tasks in industry. It was important to be fast and accurate in following preprogrammed motion requests. Handcrafting the location of the assembly line in order to avoid singularities was no problem. Today, when humans interact closely with robotic arms in everyday settings, it is much more important for robots to reach where they are asked to reach and to move in predictable ways. It is much more acceptable to slow down if necessary, rather than to simply "stop trying" in response to certain requests.
Is there a simple analogy?
A child (or for that matter, an adult) is good at one activity and finds another extremely daunting. The goal is for this child to achieve a task that relies on successful completion of both activities. As a teacher, the options are:
1. Insist on both parts being completed in a short period of time. The child's confidence is shattered and neither part gets done. In fact everything goes downhill after this. Even bystanders suffer.
2. Decide that nothing can be done about the task as a whole. Instruct the child not to attempt it. The task remains undone and the skill unlearned. The child never even finds out what was possible.
3. Explain that the task has two parts. The first part can and should be done, and will move fast and be done well. For the second part, ask first for only a start, a small piece of the job. Once the start is made, ask for a little more, something manageable. Explain that there is enough time to learn and do just that piece for now. Keep breaking the activity into parts and stepping through it piece by piece. In time, the entire task will be completed, and the child's capabilities expanded.
Method at a Glance
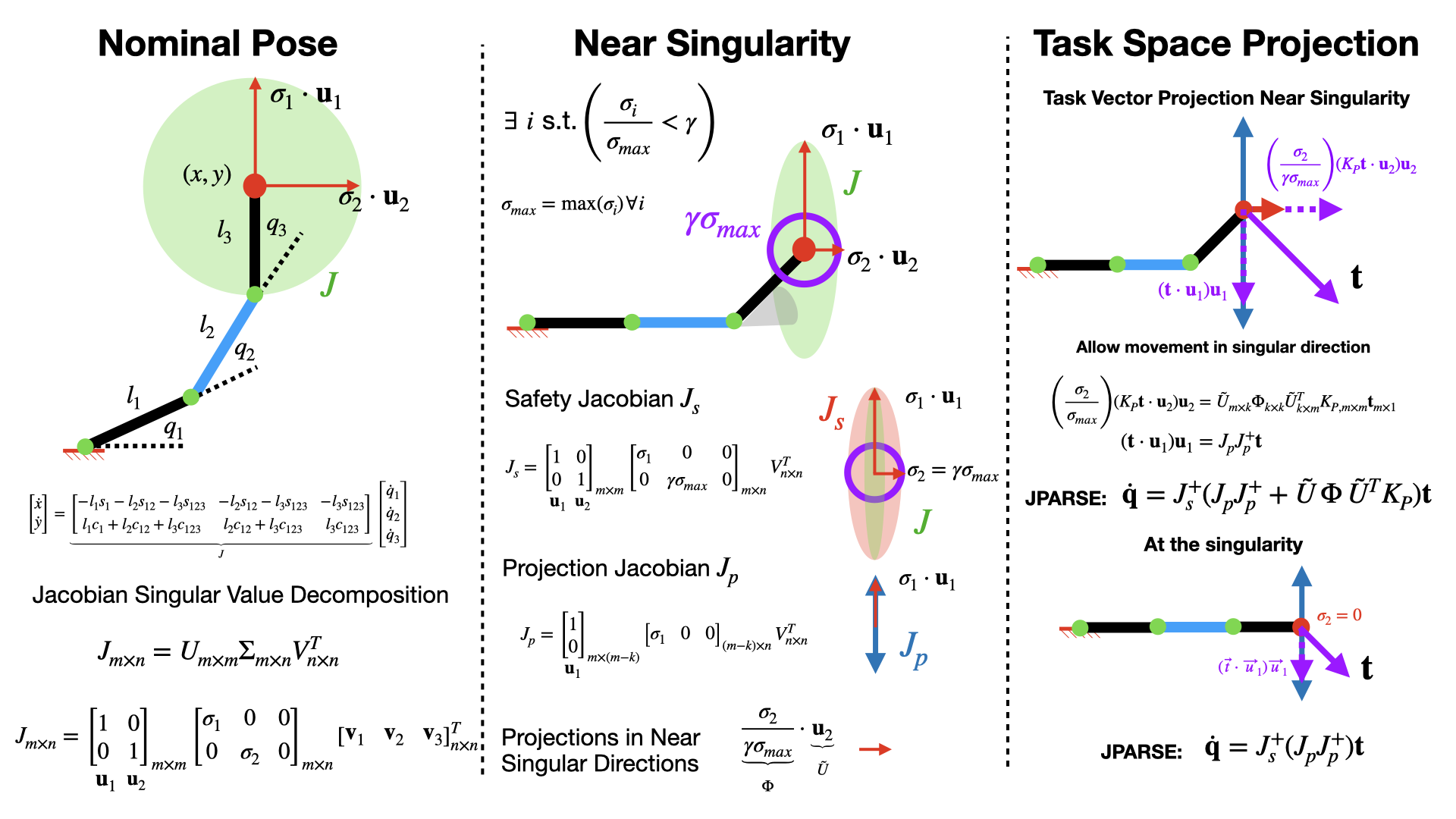
When far from singularities, the Jacobian is high-rank,
and the Manipulability Ellipsoid allows motion in any feasible direction (first column). Near singularities,
the ellipsoid contracts
along the singular direction as the Jacobian approaches low rank. J-PARSE generates a Safety Jacobian Js to
prevent further
contraction along the singular axis. The commanded vector t is projected into singular and non-singular
components, scaling the
singular direction component based on the singular value. At a true singularity (within numerical precision),
motion in singular
directions is restricted. However, with a small perturbation, J-PARSE can exit the singularity over time,
making singularities
unstable points.
Real-World Examples
Imitation Learning
Our method can be seamlessly integrated into demonstrations from imitation learning, as J-PARSE expands the
task space
in a manipulator's workspace, making extreme reaching tasks possible.
Autonomous inference on the Xarm7 with Diffusion Policy
Visual Servoing
J-PARSE can be extended to other robots, and can be used for visual servoing tasks. In the below video,
we display the Kinova Gen3 following the AprilTag, and display the manipulability measure,
a metric that describes the robot's closeness to singularity.
Kinova Gen3 following an AprilTag marker
Goal Reaching
J-PARSE allows for the smooth entry and exit out of singularity, whereas prior methods will completely
stop the robot when it gets close to a singularity by avoiding it entirely. J-PARSE embraces the
singularity.
Xarm7 reaching and exiting multiple singular poses
Simulation Examples
J-PARSE is tested on multiple robots (XArm7, Kinova Gen3, Puma 6DOF) in simulation against other
methods. Note how the leading method of DLS suffers from a steady state error even in
non-singular poses.
XArm Ellipse
XArm Line
Kinova Line
PUMA Robot J-PARSE
More Videos Coming Soon! For More Comprehensive Results, Please See Our Paper.
Interactive Game
Check out our interactive game! Drag the the pink dot to control the target pose of the robot. Using J-PARSE, the three-link manipulator will be able to enter and exit the singularity! Note that the browser will ask to "save changes" when you reload the page -- feel free to ignore this and reload.
Citation
If you find our project useful, please consider citing:
AخA
@article{guptasarma2025JParse,
title={J-PARSE: Jacobian-based Projection Algorithm for Resolving Singularities Effectively in Inverse Kinematic Control of Serial Manipulators},
author={Guptasarma, Shivani; Strong, Matthew; Zhen, Honghao; Kennedy III, Monroe},
journal={arXiv preprint arXiv:2505.00306},
year={2025}
}
